Sudoku lovers looking for the next big challenge often find themselves drawn to the powerful, intricate, and immensely satisfying Samurai Sudoku. This advanced puzzle takes traditional Sudoku and multiplies its complexity by five—literally.

In this ultimate 2025 guide, we’ll cover everything you need to know to master Samurai Sudoku:

• Clear explanation of rules
• Unique grid structure and variations
• Solving strategies for beginners and pros
• Common mistakes and how to avoid them
• Recommended books, apps, and tools
• Free printable samurai sudoku resources

What Is Samurai Sudoku?

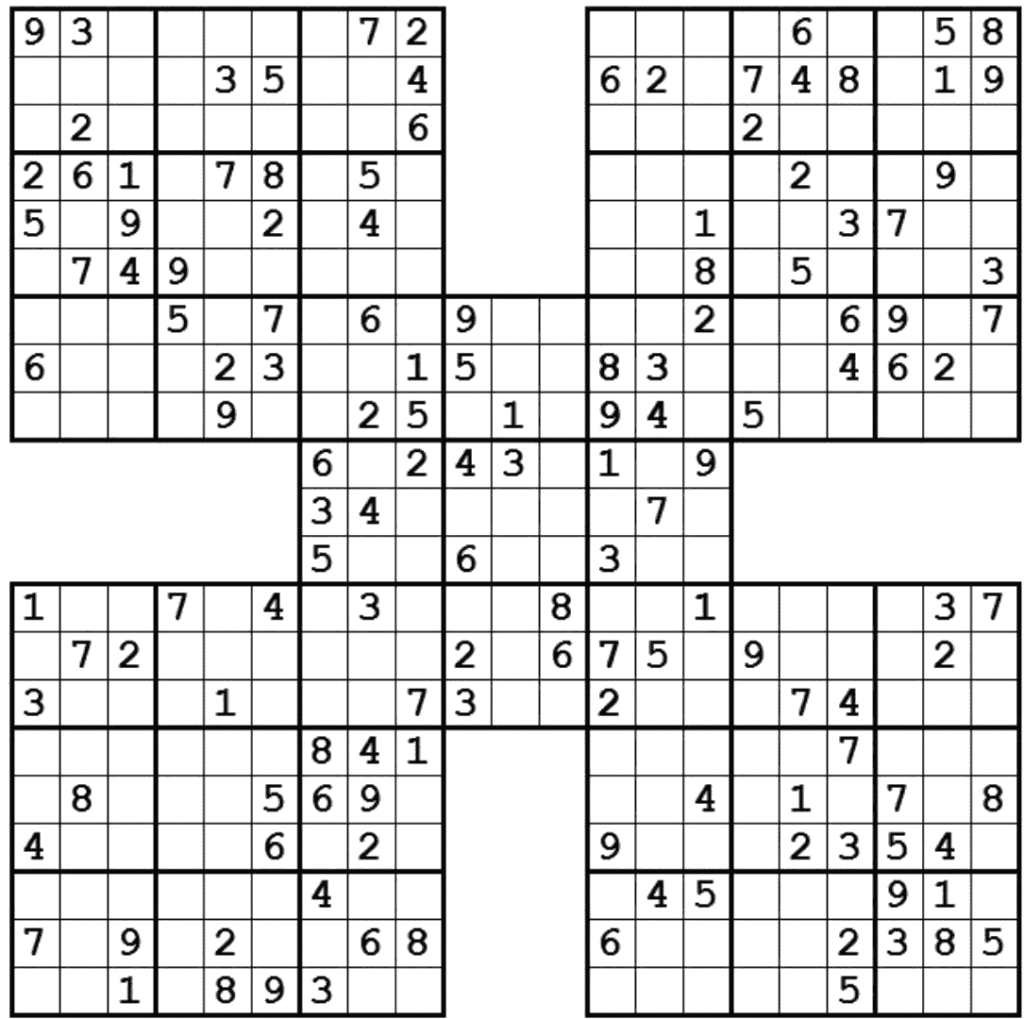
Samurai Sudoku, sometimes called Gattai-5 Sudoku or 5-grid Sudoku, is an advanced and highly engaging variant of the traditional Sudoku puzzle. Unlike the standard version, which features a single 9×9 grid, Samurai Sudoku consists of five interlocking Sudoku grids arranged in the shape of a cross. Four of these grids are positioned at each corner, and a fifth grid sits in the center, overlapping each of the outer puzzles through shared 3×3 regions. This clever overlapping design means that the puzzles are not independent—solving one grid directly influences the others.

The overall puzzle typically spans a 21×21 space, though not all of the cells are filled with numbers, since the grids share sections. The challenge lies in the interconnectedness of the grids: while each individual Sudoku follows the standard rules—every row, column, and 3×3 box must contain the digits 1 through 9 without repetition—the overlapping areas must also satisfy those same rules simultaneously for both of the connected puzzles.

This unique interdependence requires solvers to think strategically across multiple grids at once. Samurai Sudoku demands patience, logical reasoning, and careful pattern recognition. It offers a richer, more complex solving experience that appeals to seasoned Sudoku enthusiasts seeking a new level of difficulty and depth.

Key Features:

• Total size: typically 21×21 grid space
• Overlaps in 4 corner areas (3×3 each)
• Follows classic Sudoku rules (1–9, no repeats in rows/columns/boxes)

Structure & Layout of Samurai Sudoku

The structure and layout of Samurai Sudoku make it one of the most fascinating and visually distinctive logic puzzles. Unlike the traditional Sudoku, which features a single 9×9 grid, Samurai Sudoku is composed of five interlocking 9×9 grids arranged in a symmetrical cross pattern. Four of these grids occupy each corner of the overall puzzle—top left, top right, bottom left, and bottom right—while the fifth grid sits precisely in the center, overlapping with each of the outer grids. This arrangement gives the puzzle a sprawling appearance, often spanning a 21×21 cell area, although not every cell is used because the grids overlap at their corners.

Each of the five component grids follows the standard Sudoku rules: every row, every column, and every 3×3 subgrid must contain all digits from 1 to 9 without repetition. The overlapping regions are where the uniqueness of Samurai Sudoku becomes evident. Each overlap is a 3×3 subgrid shared between the central grid and one of the outer grids. This means the overlapping squares must simultaneously satisfy the logical constraints of both the connected grids. As a result, the values placed in those shared cells affect multiple areas of the puzzle at once, linking all five grids into one cohesive challenge.

Visually, the layout forms a shape that resembles a samurai’s armor or cross-blade pattern, which inspired the puzzle’s name. When viewed as a whole, it has an interconnected symmetry that is both elegant and intricate. The design ensures that solvers must move fluidly between grids, using deductions from one area to unlock progress in another.

Because of this intertwined structure, Samurai Sudoku requires more than just basic Sudoku-solving techniques. Players need to think in broader patterns, track relationships between distant parts of the puzzle, and maintain consistency across multiple grids at the same time. This complex yet harmonious structure is what gives Samurai Sudoku its enduring appeal among advanced puzzle enthusiasts.

Rules of Samurai Sudoku

Samurai Sudoku combines the familiar logic of traditional Sudoku with an added layer of complexity created by overlapping grids. While the basic rules remain the same, the interconnected structure introduces additional constraints that make solving the puzzle more challenging and strategic. Below are the detailed rules of Samurai Sudoku:

1. Structure of the Puzzle

• Samurai Sudoku consists of five 9×9 grids — one central grid and four outer grids (top-left, top-right, bottom-left, and bottom-right).
• Each outer grid overlaps the central grid through a shared 3×3 region at its nearest corner.
• The overall layout forms a large cross-shaped structure spanning 21×21 cells, though some corner areas remain empty.

2. Basic Sudoku Rules (Applied to All Grids)

• Each row, column, and 3×3 subgrid within a 9×9 grid must contain all digits from 1 to 9, without repetition.
• Numbers cannot be repeated in any single row, column, or 3×3 box within the same grid.
• Every grid operates as a standard Sudoku but is connected to the others through overlapping sections.

3. Overlapping Regions

• Each overlap (3×3 area) belongs to two grids simultaneously — the central grid and one outer grid.
• The numbers placed in these shared cells must satisfy both grids’ Sudoku conditions at the same time.
• Therefore, solving one grid affects the other four, making the puzzle interdependent.

4. Logical Consistency

• Every placement of a number must be logically deduced, not guessed.
• Each step should comply with both the local grid rules and any overlap constraints.
• Mistakes in one grid can easily disrupt multiple grids due to the shared areas.

5. Starting Clues (Given Numbers)

• The puzzle starts with several pre-filled numbers (clues) spread across all five grids.
• These clues are carefully arranged to ensure there is one unique solution for the entire puzzle.
• No external information or arithmetic is required—only logic.

6. Objective

The entire interconnected puzzle follows standard Sudoku logic rules.

Fill in all empty cells across all five grids so that:

Each row, column, and 3×3 box in every grid contains digits 1–9 once.

All overlapping regions maintain consistency between the grids.

Variants of Samurai Sudoku

Over time, the traditional Samurai Sudoku puzzle has inspired a wide range of creative and challenging variants. These versions build upon the original concept of five interlocking Sudoku grids but introduce new rules, visual elements, and logic twists that expand the depth and enjoyment of solving. Each variant adds a distinctive challenge while preserving the interconnected structure that defines Samurai Sudoku. Below are some of the most notable variants, explained in detail.

1. Jigsaw Samurai Sudoku

In Jigsaw Samurai Sudoku, the familiar 3×3 subgrids are replaced by irregularly shaped regions. These regions—sometimes called “jigsaw” or “irregular boxes”—can take on a variety of shapes while still containing nine cells each. The rule remains the same: each region must contain the digits 1 through 9, without repetition. The twist lies in how these irregular shapes disrupt the solver’s typical pattern recognition, forcing them to adapt to non-linear boundaries. When combined with the overlapping structure of Samurai Sudoku, the difficulty increases significantly. Solvers must carefully manage both the irregular regions and the shared 3×3 overlaps between grids, making this variant a true test of logical flexibility.

2. Diagonal Samurai Sudoku

Diagonal Samurai Sudoku adds another layer of complexity by applying the “Sudoku X” rule to each of the five grids. In this version, not only must each row, column, and 3×3 box contain the numbers 1 to 9, but the two main diagonals of every grid must also contain all digits 1–9 without repetition. This additional constraint drastically reduces the possible placements of numbers, creating a tighter logical web that links each grid even more strongly. Solvers must continuously check diagonal consistency across multiple grids, which makes this variant both elegant and mentally demanding.

3. Samurai Killer Sudoku

In Samurai Killer Sudoku, the overlapping Sudoku grids are enhanced with Killer Sudoku “cages”—dotted-line regions with small numerical clues that represent the sum of the digits within them. Players must fill these cages using the standard Sudoku rules and ensure that the numbers within each cage add up to the specified total, with no repeats allowed inside a cage. When these cages extend into the overlapping 3×3 zones, solvers must balance arithmetic reasoning with logical placement. This variant demands strong mental arithmetic skills and careful deduction, making it one of the most advanced Samurai versions.

4. Samurai Sudoku with Thermometers, Arrows, or Colors

Modern puzzle creators and digital Sudoku apps have introduced thematic and visually enhanced Samurai Sudokus. In these versions, additional elements such as thermometers, arrows, or colored regions appear within the grids.

• In Thermometer Samurai Sudoku, each thermometer shape has cells that must increase numerically from the bulb to the tip.
• In Arrow Samurai Sudoku, a circle with an attached arrow indicates that the number in the circle equals the sum of the digits along the arrow’s path.
• Color-based Samurai Sudoku may introduce zones of matching colors, each following special rules such as containing unique numbers or following arithmetic patterns.

These creative adaptations combine the beauty of visual design with deep logical reasoning.

How to Solve Samurai Sudoku (Step-by-Step Strategy)

Below is a detailed, pointwise step-by-step strategy for solving a Samurai Sudoku, organized in four phases. Each point is actionable—techniques to apply, what to look for, and how to handle the overlaps that make Samurai unique.

Phase 1 — Start with the Outer Grids

1. Treat each outer 9×9 as a regular Sudoku initially.
   • Scan for Naked Singles (only one candidate for a cell) and Hidden Singles (the only place for a digit in a row/column/box). Fill those first.
2. Work easy rows/columns first.
   • Focus on rows or columns that don’t touch overlap zones; these are the least constrained and often give quick fills.
3. Use box/line reduction (claiming).
   • If a candidate for a number in a 3×3 box can only appear in one row/column inside that box, eliminate that candidate from the same row/column outside the box.
4. Find pairs/triples early.
   • Identify Naked Pairs/Triples and Hidden Pairs/Triples inside boxes/rows/columns to vastly reduce candidates.
5. Keep tidy pencil marks.
   • Mark candidates for every unsolved cell. Use small numerals or a digital app’s candidate feature.
6. Prioritize progress, not completeness.
   • Finish what you can in an outer grid before moving on, but don’t get stuck trying to completely solve one outer grid if progress stalls.

Phase 2 — Identify & Exploit Overlap Zones

1. Treat each 3×3 overlap as a two-grid constraint.
   • Any number placed in an overlap must obey rules for both the central and the outer grid.
2. Translate solved digits across the overlap immediately.
   • When you place a digit in an overlap from one grid, remove that candidate from corresponding row/column/box in the other grid right away.
3. Search for “overlap singles.”
   • Sometimes a cell in the overlap becomes a Hidden Single when considering both grids simultaneously—spot and fill those.
4. Use claiming across the overlap.
   • If an outer grid limits a number in the overlap to a specific row/column, you can eliminate that number from that row/column in the central grid (and vice versa).
5. Mark overlap-dependent candidates.
   • Annotate candidates that are valid only because of outer-grid state; these are high-value candidates to re-check later.

Phase 3 — Work the Central Grid Intensively

1. Switch focus to the center early and often.
   • The central grid connects to all four outers; progress here multiplies across the puzzle.
2. Apply medium/advanced techniques:
   • X-Wing / Swordfish: Look for candidate patterns across rows/columns that force placements or eliminations.
   • XY-Wing / XYZ-Wing and Chains: Use these to eliminate candidates that are otherwise hard to remove.
3. Use inter-grid logic chains.
   • A chain that starts in the center and ends in an outer grid via overlaps can produce eliminations not visible inside a single grid.
4. Constantly push changes outward.
   • Every number you fix in the central grid should be propagated immediately into outer grids’ candidate lists.

Phase 4 — Cross-Grid Inference & Iteration

1. Alternate grids rather than finishing one at a time.
   • Cycle between outer → overlap → center → another overlap. Small changes often unlock new singles elsewhere.
2. Look for eliminations caused by remote interactions.
   • A placement in one outer grid might, via overlaps, create a hidden single in a different outer grid. Always re-scan all five grids after a batch of placements.
3. Use double-checking to avoid errors.
   • Re-verify overlaps after several moves—errors propagate quickly in Samurai.
4. Apply coloring and multi-color chains for difficult eliminations.
   • Coloring techniques help when you have two-color candidate chains across multiple grids; contradictions reveal true placements.
5. When stuck, hunt for advanced patterns.
   • Look for ALS (Almost Locked Sets), remote pairs, or wings that cross overlap boundaries. These advanced tactics often crack the hardest puzzles.
6. Final polishing:
   • As the grid nears completion, switch to strict candidate elimination and verification—resolve any remaining naked/hidden pairs and finish with singles.

Practical Tips & Workflow

• Use an app or mark grids with colors so you visually separate the five grids and quickly see overlap effects.
• Work in small batches of moves and re-scan all overlaps; that reduces mistakes.
• Keep a “recent changes” mental or written list — if a contradiction appears, you’ll know which recent placements to review.
• Be patient: Samurai puzzles are designed to reward cross-grid insight rather than brute force.

Follow these phase-by-phase points, switch focus frequently, and always propagate overlap information immediately. That disciplined, iterative approach is the key to solving Samurai Sudoku reliably.

Advance Samurai Sudoku Solving Techniques

Here, we have explained the advance Samurai Sudoku solving techniques in detail. These techniques are powerful when used together — learn to switch between them depending on which part of the five-grid layout you’re working.

1. Naked & Hidden Pairs / Triplets

What they are

• Naked pair: two cells in the same house (row, column, or box) contain exactly the same two candidates (e.g., {2,7} and {2,7}). No other cell in that house can be 2 or 7.
• Hidden pair: two digits appear only in the same two cells of a house among many candidates (those cells may have other candidates), so all other candidates in those two cells can be removed.
• The same idea scales to triplets (three cells, three digits).

How to spot them

1. Scan a house and look for cells with exactly 2 or 3 candidates.
2. Check candidate lists: if exactly two cells cover the same two digits, mark a naked pair.
3. If two digits appear only in two cells (even though those cells have extra candidates), you have a hidden pair.

Applying in Samurai

• Inside overlap zones: because an overlap belongs to two grids, a naked/hidden pair found in the overlap restricts both grids simultaneously. For example, if an overlap box has a naked pair {3,8}, remove 3 and 8 from the corresponding rows/columns in both connected grids.
• Cross-grid exploitation: a hidden pair in an outer grid’s row might force eliminations in the central grid via the overlapping columns.

Tip/Pitfall

• Always update both grids after changes in the overlap. Forgetting to propagate eliminations is the most common mistake.

2. X-Wing & Swordfish

What they are

• X-Wing: a pattern of candidate X in two rows and two columns forming a rectangle where X appears in exactly two cells in each involved row and column. One of the two columns must contain X in the four candidate cells, allowing elimination of X from other cells in those columns.
• Swordfish: extends X-Wing to three rows and three columns with the same logic.

How to spot them

1. Pick a candidate digit (e.g., 5).
2. Look at the rows: find 2 (X-Wing) or 3 (Swordfish) rows where candidate 5 appears only in the same set of columns.
3. If the columns match the pattern, you can eliminate candidate 5 from other cells in those columns (or rows, depending on orientation).

Applying in Samurai

• Row/column spread across grids: Samurai’s outer and central grids share rows/columns only via overlaps; however, an X-Wing can form across grid boundaries when candidate occurrences line up across an overlap. Example:
  • Candidate 5 appears only in columns 4 and 8 of outer-top-left grid’s rows 2 & 7; those same columns align with candidate 5 positions in the central grid’s corresponding rows — you may form an X-Wing spanning two grids.
• Use on long vistas: treat any continuous row/column segment across the larger 21×21 visual (ignoring empty corner cells) as a search field for these patterns.

Tip/Pitfall

• Swordfish is more subtle and often misidentified. Verify that candidate positions in all three rows are confined to the same three columns (and vice versa) before eliminating.

3. Coloring & Chains

What they are

• Coloring: use two colors to mark candidate chain implications for a single digit. If a contradiction arises on one color, the other color must be true.
• Chains (e.g., XY-chain): link bivalue cells (cells with 2 candidates) into a chain such that if one end value were true it forces a contradiction, allowing elimination elsewhere.

How to do coloring

1. Choose a digit (e.g., 6).
2. Find strong links (cells in the same house where the digit must be in one of two cells). Color one cell color A and the other color B, propagate linked strong/weak links alternating colors.
3. If two cells of the same color appear in the same house, that color is false and you can eliminate that color’s candidates—accept the other color.

Applying in Samurai

• Central zones: coloring helps in the central grid where many implications cross to the outers. If a color implies a contradiction in an outer grid via an overlap, you can resolve a web of candidates instantly across multiple grids.
• Chains across overlaps: construct an XY-chain that starts in an outer grid, passes through an overlap bivalue, and ends in a different outer — such chains can eliminate candidates that no single-grid technique can.

Tip/Pitfall

• Keep your color/chain bookkeeping tidy. In paper puzzles use two highlighter colors; in apps use built-in coloring. Miscolored chains lead to false conclusions.

4. Symmetry Detection

What it is

• Many published Samurai puzzles are constructed with aesthetic symmetry. Recognizing symmetrical clue placement can sometimes suggest where digits are likely to appear or narrow candidate patterns.

How to use it

1. Look at the overall puzzle layout for rotational or mirror symmetry.
2. If one outer grid has a specific constraint or unique clue arrangement, check the symmetric position in the opposite outer grid for similar candidate behavior.
3. Use symmetry as a heuristic — not a rule. It suggests areas to inspect for similar patterns (e.g., mirrored hidden singles).

Applying in Samurai

• Anticipate placements: symmetry rarely gives a direct solution, but it can guide where to hunt for pairs/patterns early on.
• Cross-checks: if two symmetric areas resist different logical moves, re-check pencil marks — asymmetry in candidates often signals a missed elimination.

Tip/Pitfall

• Don’t assume symmetry always holds for solutions; constructors sometimes place asymmetrical clues intentionally to increase difficulty.

5. Box-Line Reduction (Box/Line Interaction)

What it is

• If all candidate positions for digit D in a 3×3 box lie in one row (or column), then D can be eliminated from other cells in that row (or column) outside the box. The reverse (line claiming) is also true.

How to spot it

1. In a 3×3 box, list cells that can contain digit D.
2. If they all fall within the same row (or column) of that box, then eliminate D from other cells in that row/column outside the box.

Applying in Samurai

• Overlaps are prime territory: an outer grid’s box that overlaps the center may have candidate D confined to the overlap row — that lets you eliminate D in the central grid’s corresponding row/column and in the outer grid outside the box simultaneously.
• Chain of reductions: box-line reductions often unlock hidden singles in the connected grid; use them early when scanning overlap boxes.

Tip/Pitfall

• Box-line reductions are deceptively strong in Samurai because a single elimination often cascades across multiple grids. Always propagate eliminations to all affected grids immediately.

Final Practical Advice

Use an app with candidate, coloring, and grid-highlighting features when tackling extreme Samurai puzzles — they make applying these techniques far less error-prone.

Combine techniques: e.g., find a naked pair then use coloring to force a chain that yields an X-Wing.

Work in short iterative cycles: apply a few techniques, propagate, then re-scan overlaps.

Common Mistakes to Avoid while solving Samurai Sudoku

Below are the four mistakes, each explained with why it matters, how it shows up, how to detect it, and concrete fixes you can apply while solving Samurai Sudoku.

1) Ignoring overlap influence from other grids

• Why it matters: Overlap cells belong to two grids at once — a placement or elimination in one grid immediately constrains the other. Ignoring that link lets contradictions and missed deductions accumulate.
• How it shows up: You solve part of an outer grid, then later find a conflicting digit in the overlap of the center grid (or miss a hidden single that the overlap reveals).
• How to detect: If the same cell is treated differently when viewing each grid separately, you’re ignoring overlap rules. Frequent backtracking after many moves is a sign.
• Fixes / Preventive habits:
  • Always propagate every placement in an overlap to both grids immediately.
  • When you pencil-mark candidates, mark overlap candidates with a small flag (e.g., “o”) so they’re rechecked after any change.
  • After any batch of moves, do a quick scan of all four overlaps before continuing.

2) Filling the central grid too early without support from corners

• Why it matters: The center grid typically has fewer givens; premature guesses there can force errors across four grids because the center ripples outward.
• How it shows up: You place several central numbers to make progress, then later find they contradict well-established outer placements.
• How to detect: High number of contradictions or frequent revisiting of the same central cells indicates over-eagerness.
• Fixes / Preventive habits:
  • Use the outer grids to generate strong constraints first — solve obvious outer singles/pairs before committing many center placements.
  • Treat center placements as provisional unless justified by overlapping evidence (i.e., confirmed by outer-grid logic).
  • Use candidate-only work in the center: avoid fixing a number unless it’s a naked/hidden single, or proven by strong-chain techniques.

3) Misaligning rows/columns between printed grids

• Why it matters: Samurai puzzles are visually larger than a single 9×9; misreading alignment between printed sections leads to wrong eliminations or misplaced X-Wings.
• How it shows up: You eliminate a candidate from the wrong column because you miscounted the overlap offset, or you think two cells are in the same row when they are not.
• How to detect: Repeated “why didn’t that elimination help?” moments or discovering that supposed aligned candidates don’t actually share a house.
• Fixes / Preventive habits:
  • Physically mark or shade the overlap columns/rows on your printout before starting (use highlighter or a ruler).
  • Number the global columns/rows across the whole 21×21 visual (e.g., label columns 1–21) so you always know alignment.
  • If using paper, fold lightly at overlap boundaries or use sticky tabs; if using an app, enable grid-highlighting for overlaps.

4) Forgetting rules on repeated numbers in 3×3 boxes—especially across junctions

• Why it matters: Overlaps can create “junction” areas that are part of two 3×3 boxes (one from the center, one from an outer). It’s easy to forget that each of those boxes still must contain 1–9 without repeats.
• How it shows up: You inadvertently place the same number twice within a box because one occurrence was considered “belonging to the other grid,” or you fail to eliminate candidate duplicates in the shared 3×3 region.
• How to detect: If you ever find a repeated digit inside what should be a single 3×3 (after considering both grids), you’ve missed this rule. Also watch for overlaps where both grids seem to “allow” the same candidate cell.
• Fixes / Preventive habits:
  • Always visualize each 3×3 box by its actual membership — if it sits inside an overlap, remember it participates in two separate 3×3 constraints (center’s box and outer’s box).
  • When placing a number in an overlap, run a micro-check: verify that number does not already appear in either box, either box’s rows, or columns.
  • Maintain disciplined candidate lists in the overlap; eliminate immediately from both boxes when a digit is fixed.

Quick Checklist to Avoid All Four Mistakes

• After every placement in an overlap: propagate to both grids.
• Before fixing a center digit: confirm by outer-grid evidence or advanced technique.
• Mark or number the global grid to prevent misalignment.
• After any move: verify all affected 3×3 boxes (including those at junctions) for repeats.
• Work in short cycles and re-scan overlaps frequently — small, frequent checks beat big, error-prone jumps.

Keeping these habits will drastically reduce errors and make your Samurai solving smoother and faster.

Free Printable Samurai Sudoku (High Quality)

Many puzzle enthusiasts prefer solving Samurai Sudoku on paper. Here are trusted resources for free printable Samurai Sudoku puzzles:

• SamuraiSudoku.com – Classic 5-grid puzzles
• sudokutimes.com – Custom difficulty levels
• SudokuDownload.org – Downloadable PDFs

Make sure you select medium to hard difficulty puzzles for true skill-building.

Best Apps for Samurai Sudoku

In 2025, these are the top-rated Sudoku apps with Samurai support:

1. Sudoku.com by Easybrain – Includes overlapping Sudoku variants
2. SudokuTimes.com – Option of different Difficulty Levels
3. Killer Sudoku by Logic Wiz – With Samurai Killer mode
4. Good Sudoku by Zach Gage – AI assistant + minimalist design

Best Books for Samurai Sudoku Practice

If you’re serious about mastering Samurai Sudoku, these books are highly recommended:

1. “Samurai Sudoku 500 Hard Puzzles” by Djape
2. “Samurai Sudoku Collection” by Puzzle Genius
3. “Ultimate Sudoku Variants” by Conceptis Puzzles

Look for books labeled “Overlapping Sudoku” or “5-Grid Sudoku” for comprehensive practice.

⚔️ Want to try Your skills right now !!! Click Here! 👈

FAQs On Samurai Sudoku

Q1. What is Samurai Sudoku?
Ans: Samurai Sudoku is a complex, logic-based puzzle that merges five overlapping 9×9 Sudoku grids into a single interconnected layout. The central grid overlaps with each of the four outer grids through shared 3×3 boxes, forming a large cross-shaped puzzle.

Q2. How does Samurai Sudoku differ from regular Sudoku?
Ans: Unlike regular Sudoku, which has only one 9×9 grid, Samurai Sudoku features five interlinked grids. The overlapping zones connect these puzzles, requiring players to think across multiple grids simultaneously.

Q3. What are the basic rules of Samurai Sudoku?
Ans: The rules are the same as classic Sudoku—each row, column, and 3×3 box must contain digits 1 to 9 without repetition. Overlapping sections must satisfy both grids they connect, following the same rules in each.

Q4. What is the total grid size of Samurai Sudoku?
Ans: The overall puzzle layout spans a 21×21 grid area, though not every square is filled because the grids overlap at the corners.

Q5. How many Sudoku grids make up Samurai Sudoku?
Ans: Samurai Sudoku consists of five interlocking 9×9 grids—one central grid and four corner grids arranged around it.

Q6. Is Samurai Sudoku harder than normal Sudoku?
Ans: Yes. Samurai Sudoku is more challenging due to its interconnected grids and overlapping regions, which demand advanced logical thinking and cross-grid reasoning.

Q7. How should beginners start solving Samurai Sudoku?
Ans: Start with the outer grids that have more given numbers. Work on easy placements before focusing on overlap zones and finally the central grid.

Q8. What are overlap zones in Samurai Sudoku?
Ans: Overlap zones are the shared 3×3 sections where the central grid connects with each outer grid. The numbers placed here must follow the Sudoku rules for both grids simultaneously.

Q9. What are some strategies to solve Samurai Sudoku?
Ans: Use classic Sudoku techniques like Naked Pairs, X-Wing, and Box-Line Reduction. Focus on overlaps early and cross-check digits between connected grids frequently.

Q10. Can Samurai Sudoku be solved logically without guessing?
Ans: Yes. Like standard Sudoku, Samurai Sudoku can always be solved through pure logic without guessing if the puzzle is correctly designed.

Q11. What are the most common mistakes in Samurai Sudoku?
Ans: Common mistakes include ignoring overlap influences, filling the central grid too early, misaligning rows or columns, and repeating digits across junction boxes.

Q12. Are there different types of Samurai Sudoku variants?
Ans: Yes. Popular variants include Jigsaw Samurai Sudoku, Diagonal Samurai Sudoku, Samurai Killer Sudoku, and versions with thermometers, arrows, or colored regions.

Q13. Can Samurai Sudoku be played online?
Ans: Absolutely. Many puzzle websites and Sudoku apps offer interactive Samurai Sudoku puzzles with digital highlighting and candidate features.

Q14. How long does it take to solve Samurai Sudoku?
Ans: The time varies based on difficulty and experience. A skilled player might solve an easy Samurai Sudoku in 30–60 minutes, while difficult ones can take several hours.

Q15. Why is it called Samurai Sudoku?
Ans: The puzzle’s layout resembles a samurai’s armor or crossed swords, inspiring the name “Samurai Sudoku.” It symbolizes strength, strategy, and precision—qualities required to solve it.

Is Samurai Sudoku Worth It?

If you’re looking for a rewarding brain workout, few puzzles can match the elegance and challenge of Samurai Sudoku. It combines everything Sudoku solvers love—logic, complexity, and strategic deduction—multiplied fivefold.

Whether for casual fun or competitive training, mastering Samurai Sudoku is a worthy pursuit in 2025.